PRACTICAS DE
METODOS CUANTITATIVOS
Teoría
de la decisión:
1. Una empresa está
considerando si introduce un nuevo producto al mercado
o lo abandona. La introducción del producto tendría
un costo de $50.000. Considera que existe una probabilidad
de 0.6 de que tenga una aceptación rápida
por parte del consumidor y de 0.4 de que la aceptación
sea lenta. Si la aceptación del producto fuera
rápida podría avanzar con su comercialización
o no continuar, en cuyo caso perdería los costos
de la introducción. Si avanza existen las siguientes
probabilidades con respecto a las ventas: 50% de ganar
$350.000, 30% de ganar $250.000 y 20% de perder $50.000,
esto sin incluir los costos de introducción.
Si la aceptación del producto fuera lenta podría
avanzar con su comercialización o no continuar,
en cuyo caso perdería los costos de la introducción.
Si avanza existen las siguientes probabilidades con
respecto a las ventas: 30% de ganar $250.000, 60% de
perder $50.000 y 20% de perder $100.000, esto sin incluir
los costos de introducción.
a. Construya un árbol de decisión que
modele este problema.
b. ¿Qué decisión debe tomarse?
¿Cuál es la utilidad esperada?
c. ¿Qué consideraciones con relación
al riesgo pueden realizarse al tomar esta decisión?
2. Un fabricante de
tónico para el cabello está considerando
la producción de un nuevo producto de peluquería.
La utilidad incremental es de $10 por unidad y la inversión
necesaria en equipo es de $150.000. El estimado de la
demanda es como sigue:
|
Unidades |
Probabilidad |
20000 |
0.15 |
40000 |
0.20 |
60000 |
0.25 |
80000 |
0.25 |
100000 |
0.15 |
El fabricante tiene
la opción de seguir con el producto actual que
le representa ventas de 2.500 unidades con una utilidad
de $5.5/unidad sin publicidad, con la opción
de que si destina $24.000 en publicidad podría,
con una probabilidad de 80% conseguir ventas de 5.500
unidades y de un 20% de que éstas sean de 4.000
unidades.
a.
Construya un árbol de decisión que
modele este problema.
b. ¿Qué decisión debe tomarse
según el criterio de la utilidad esperada?
¿Cuál es la utilidad esperada?
c. ¿Qué consideraciones pueden hacerse
con respecto al riesgo? Comente.
Programación
lineal:
1. Una persona decide
entre el consumo de dos alimentos, cuyos precios y contenidos
nutritivos se dan a continuación, al igual que
el requerimiento mínimo de cada uno de estos
nutrientes.
| |
Alimento
A |
Alimento
B |
Requerimiento
diario |
| Precio |
¢ 0.60 |
¢ 1.00 |
| Calcio |
10 |
4 |
20 |
| Proteínas |
5 |
5 |
20 |
| Vitamina A |
2 |
6 |
12 |
¿Cuál
combinación de los dos alimentos satisface las
necesidades diarias de nutrientes y ocasiona el menor
costo?
a.
Plantee el modelo de programación lineal
del problema.
b. Grafique la situación y señale
la región factible.
c. Señale las soluciones factibles básicas
y diga cuál de ellas es la óptima.
2. La empresa El Insecto
Infeliz fabrica dos tipos de insecticidas y cada uno
requiere de una técnica diferente de fabricación.
El insecticida A requiere 18 horas de mezclado, 9 horas
de proceso y produce una utilidad incremental de ¢400
cada litro. El insecticida B requiere 3 horas de mezclado,
4 horas de proceso y produce una utilidad incremental
de ¢200 por litro. Se dispone de 800 horas para
mezclado y 600 horas para proceso cada mes. Se ha pronosticado
que la demanda mensual del insecticida A no es más
de 80 litros y para el B no más de 150 litros.
a.
Formule este problema como un modelo de programación
lineal (escriba función objetivo y restricciones).
b. Resuelva el problema por el método gráfico.
3. Una fábrica
elabora 2 productos, A y B. Cada uno de ellos debe ser
procesado en 2 máquinas diferentes. Una máquina
tiene capacidad disponible 24 horas/día y la
otra 16 horas/día. Cada unidad del producto A
requiere de 2 horas en cada máquina. Cada unidad
del producto B necesita de 3 horas en la primera máquina
y de una en la segunda. La utilidad incremental es de
$6 por unidad de A y $7 por unidad de B. La fábrica
puede vender tantas unidades de ambos productos como
pueda. El objetivo de la empresa es maximizar las utilidades.
¿Cuántas unidades debe producir de cada
producto?
a.
Formule este problema como un modelo de programación
lineal (escriba función objetivo y restricciones).
b. Resuelva el problema por el método gráfico.
PERT/CPM
1. La siguiente tabla
representa un proyecto que debe programarse utilizando
el PERT:
| Actividad
|
Predecesor
inmediato
|
Tiempo
(días)
|
a |
m |
b |
A |
- |
1 |
3 |
5 |
B |
- |
1 |
2 |
3 |
C |
A |
1 |
2 |
3 |
D |
A |
2 |
3 |
4 |
E |
B |
3 |
4 |
11 |
F |
C, D |
3 |
4 |
5 |
G |
D, E |
1 |
4 |
6 |
H |
F, G |
2 |
4 |
5 |
a.
Dibuje la red.
b. ¿CuáI es la ruta crítica?
c. ¿Cuál es el tiempo esperado para
la terminación del proyecto?
2. Con respecto a las
actividades de un proyecto se tiene la siguiente información
y conteste las preguntas siguientes:
|
Actividad |
Tiempo
|
Más
optimista |
Más
probable |
Más
pesimista |
A |
8 |
10 |
14 |
B |
7 |
9 |
16 |
C |
0 |
0 |
0 |
D |
2 |
2 |
2 |
Con base en la tabla
anterior marque con una (X) la opción correcta:
a.
Una actividad ficticia es:
( ) A ( ) B ( ) C ( ) D
b. El tiempo esperado
de la actividad B es:
( ) 14.75 ( ) 9 ( ) 1.33 ( ) 16
c. La desviación
estándar de la actividad D es:
( ) 0 ( ) 2 ( ) 32 ( ) 12
3. Se tiene la siguiente
red relacionada con un proyecto:
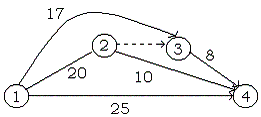
Con base en la gráfica
anterior marque con una (X) la opción correcta:
a.
La holgura del evento 3 es:
( ) 0 ( ) 17 ( ) 5 ( ) 22
b. La ruta crítica
es:
( ) 1, 4
( ) 1, 2, 4
( ) 1, 3, 4
( ) 1, 2, 3, 4
c. El tiempo esperado
del proyecto y su desviación estándar
es
( ) 30, 2.13
( ) 25, 2.33
( ) 34, 2.33
( ) 2.13, 30
4. Suponga que Ud.
desea construir una casa, y entonces contrata un constructor.
Ud. quiere saber si la casa podrá estar terminada
dentro de 4 meses, y de acuerdo con sus muchos años
de experiencia el constructor le responde:
"Todo empieza con la limpieza del terreno, en eso
se puede durar unos 2 días, luego viene el trazado,
que también puede durar otros dos días.
Si todo sale bien cada una de estas dos actividades
las terminaría en un día, pero si no,
podría retrasarme dos días.
Luego viene la excavación, que puedo durar de
2 a 7 días, seguramente duro unos 4 días,
para luego iniciar con los cimientos, que me demora
unos 7 días, si el clima es bueno, tal vez 4
días, pero si llueve duraría 12 días.
Cuando eso esté listo puedo empezar con el levantado
de las paredes y las vigas, para el tamaño de
la casa que Ud. quiere, lo más probable es que
se tarde 21 días, eso está entre 18 a
30 días. Después vienen los techos, que
duramos de 7 a 12 días, unos 10 días mejor.
Y es que hasta que esto no esté listo no puedo
empezar con la instalación eléctrica,
ni los cielorrasos ni terminar los muros. En lo eléctrico
se duran 2 días, ahí no hay retraso. En
los cielorrasos se tarda de 4 a 10 días, unos
6 para ser más preciso. Terminando los muros
duro de 10, 11 o 12 días, no más, porque
los muros deben estar listos para chorrear los contrapisos,
en eso se duran de 6 a 10 días, digamos que 8.
Y es que sino están listos no puedo poner los
pisos, que es rápido, de 5 a 10 días,
unos 8.
Veamos, ¿qué falta? La carpintería,
tienen que estar terminados los pisos y los cielorasos,
y en eso se me van unos 8 días siendo optimista,
tal vez 10, en realidad no más de 12. Para finalmente
empezar a pintar, la parte de afuera se podía
haber pintado una vez que estuvieran listos los techos,
pero adentro debe haberse finalizado toda la carpintería
y la electricidad. Cuando se termina de pintar, entonces
queda la limpieza final. En pintar adentro se gasta
de 2 a 6 días, unos 4 en promedio, y afuera igual.
La limpieza tarda unos 3, o 4, o 5 días".
Con base en esa información:
a.
Elabore una tabla en la que muestre la lista de
actividades, sus tiempos y sus precedencias.
b. Calcule el tiempo esperado y la variancia de
cada actividad.
c. Construya la red de actividades tipo CPM.
d. Calcule la ruta crítica.
e. ¿Cuántas semanas se dura construyendo
la casa?
f. ¿Cuál es la probabilidad de terminar
antes de 16 semanas, si se trabajan 5 días
a la semana?
g. ¿Cuál es la probabilidad de durar
más de 20 semanas?
h. ¿Valdrá la pena contratar obreros
extra para pintar el exterior?
i. ¿Qué ocurre con el tiempo de terminación
del proyecto si en la instalación eléctrica
se dura tres días más de lo previsto?
j. Si Ud. quiere terminar el proyecto una semana
antes ¿Qué podría hacer? ¿Qué
implicación tiene esa decisión?
Pronósticos
1. Considere la siguiente
serie de tiempo:
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Y |
10 |
17 |
19 |
31 |
20 |
27 |
29 |
41 |
30 |
37 |
39 |
51 |
Con base en los datos
anteriores conteste:
a.
Pronostique el periodo 13 por el método del
último valor.
b. Pronostique el periodo 13 por el método
de promedios móviles (use el n que crea más
apropiado).
c. Pronostique el periodo 13 por el método
de suavizamiento exponencial (use el alfa que crea
más apropiado).
d. Pronostique el periodo 13 por el método
de regresión lineal.
e. Calcule la desviación absoluta media de
los 4 resultados anteriores.
f. ¿Cuál método de pronóstico
seleccionaría usted? Explique.
g. Comente los resultados. ¿De verdad cree
usted que su pronóstico es cierto? Explique.
2. Suponga que cuenta
con la siguiente información relacionada con
la demanda de un determinado artículo: (datos
en miles)
|
Año |
Trimestre
|
1 |
2 |
3 |
4 |
1998 |
45.0 |
31.0 |
23.7 |
78.2 |
1999 |
46.5 |
32.3 |
25.6 |
77.5 |
2000 |
48.6 |
34.5 |
30.1 |
79.8 |
2001 |
49.3 |
35.6 |
32.3 |
79.9 |
a.
Grafique la serie de datos en forma trimestral y
comente su comportamiento.
b. Use regresión lineal simple para pronosticar
la demanda del año 2002.
c. Use suavizamiento exponencial para pronosticar
la demanda anual del 2002.
d. Calcule la desviación absoluta media para
los dos pronósticos anteriores para los datos
anuales. ¿Cuál pronóstico es
mejor, según el criterio de la DAM?
e. Con relación a la regresión lineal,
calcule el coeficiente de determinación e
interprete el resultado.
f. Calcule los intervalos de confianza del 95% para
la estimación obtenida con la regresión
lineal e interprételos.
g. A partir de los resultados obtenidos en la regresión,
use promedio móviles (calculando índices
estacionales) para pronosticar la demanda trimestral
del año 2002.
Inventarios
1. Una empresa elabora
un producto que requiere una pieza importada. La pieza
tiene un costo de ¢2.500 la unidad. Se estima un
costo de hacer el pedido de ¢3.000, pues incluye
el envío de faxes hasta Japón y la elaboración
de la orden es complicada. El costo de mantenimiento
del inventario se aproxima de acuerdo con la tasa de
interés pasiva vigente en el mercado de un 17%.
a. Calcule el tamaño óptimo de pedido
si se espera una demanda anual de 14.000 unidades del
producto.
b. Calcule el total de costo relevante al nivel del
pedido óptimo.
2. Una empresa produce
un artículo que requiere 4 tornillos especiales
que deben ser importados. Para el próximo año
se espera vender 600 unidades de producto por mes. El
proveedor extranjero vende cada docena de tornillos
en $1.05 si la cantidad comprada es inferior a 25.000
tornillos al año, y en $1 si la cantidad excede
los 25.000 tornillos. Para poder importar se debe pagar
algunos impuestos, seguros y el transporte que se han
estimado en $0.6 por docena de tornillos importada.
El plazo de entrega es de 42 días después
de realizado el pedido. La realización de un
pedido implica que el gerente de producción deba
emplear 25 minutos cada vez que se ordena, y 20 minutos
de la secretaria. El gerente gana ¢400.000 por
mes (trabaja en promedio 22 días por mes, 8 horas
diarias) y la secretaria gana ¢6.000 por día.
Se han estimado otros costos por ¢510 por pedido.
El costo de mantenimiento del inventario se estima con
relación a la tasa de interés pasiva,
que actualmente es de 18% como costo de oportunidad
del capital más $0.01 por tornillo. Actualmente
el tipo de cambio es de ¢546 por dólar.
Calcule:
a.
La cantidad económica de pedido.
b. El costo anual del inventario.
c. Número de órdenes en un año.
d. Número de días entre órdenes.
e. El punto de reorden.
Modelos
de líneas de espera
1. A un banco llega
clientes a una tasa de 30 por hora, y cada cajero puede
atender a 12 por hora. Si el banco tiene 3 cajas y se
hacen 3 filas, una para cada caja. Calcule la longitud
promedio de la cola y el tiempo medio del sistema. Suponga
tiempos de servicio exponenciales y que las llegadas
de los clientes son aleatorias.
2. Un médico
que puede atender a cuatro personas cada hora, y los
pacientes llegan a una tasa de 3 cada hora. Determine:
a. La longitud promedio de la cola. b. El tiempo de
espera promedio. c. La longitud promedio de de la línea
del sistema. d. Tiempo de espera promedio del sistema.
e. La tasa de utilización de la instalación.
e. La probabilidad de que la cola sea de tres personas
o más. Suponga que los tiempos de servicio siguen
una distribución exponencial y que las llegadas
son aleatorias.
3. Una empresa está
analizando si debe contratar para atender las llamadas
de sus clientes 1, 2 o 3 operadoras. Una operadora puede
atender, en promedio, cinco llamadas por minuto (con
distribución Poisson). Se espera recibir llamadas
en forma aleatoria con una tasa promedio de 8 por minuto.
¿Cuántas operadoras debe contratarse para
que las llamadas se contesten, en promedio, en 15 segundos?
(12 puntos).
4. El gerente de un
banco estudia la posibilidad de instalar una servicio
de autobanca para atender a sus clientes, los cuales
se espera que lleguen a una tasa de 15 por hora. El
cajero que estará en la ventanilla podrá
atender a uno cada tres minutos. Calcule:
a.
La tasa de utilización del cajero
b. Número promedio de clientes en fila de
espera.
c. Número promedio de clientes en el sistema.
d. Tiempo promedio de espera en la fila.
e. Tiempo promedio de espera en el sistema.
f. ¿Qué decisión debería
tomarse si se quiere que la probabilidad de que
no haya más de tres automóviles en
el sistema sea del 95%?
5. Suponga que se tiene
una tasa de llegada de 50 por hora y que la tasa de
servicio es de 80 por hora.
a.
¿Cuál es la probabilidad de que haya
3 clientes en el sistema?
b. ¿Cuál es el número medio
de clientes en el sistema, esperando o recibiendo
el servicio.
c. ¿Cuál es el tiempo medio de espera
del que llega a la cola?


